The Barnsley Fern

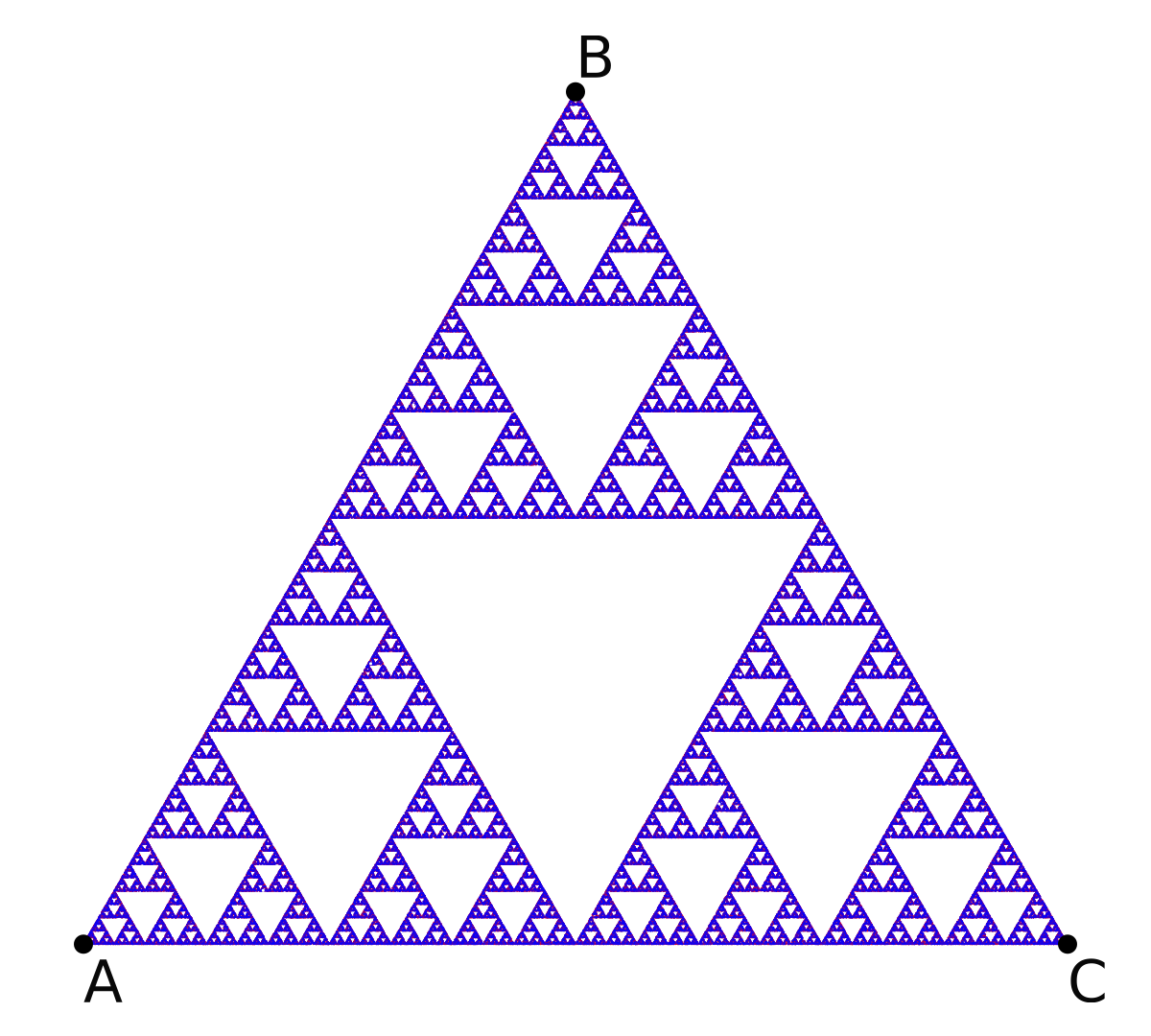
At the end of the chapter on Iterated Function Systems, we introduced two separate attractors: the Sierpinski triangle, and a uniform two-dimensional square, shown below with their corresponding Hutchinson operator.

Hutchinson Operator Attractor
Sierpinsky Triangle Chaos Game
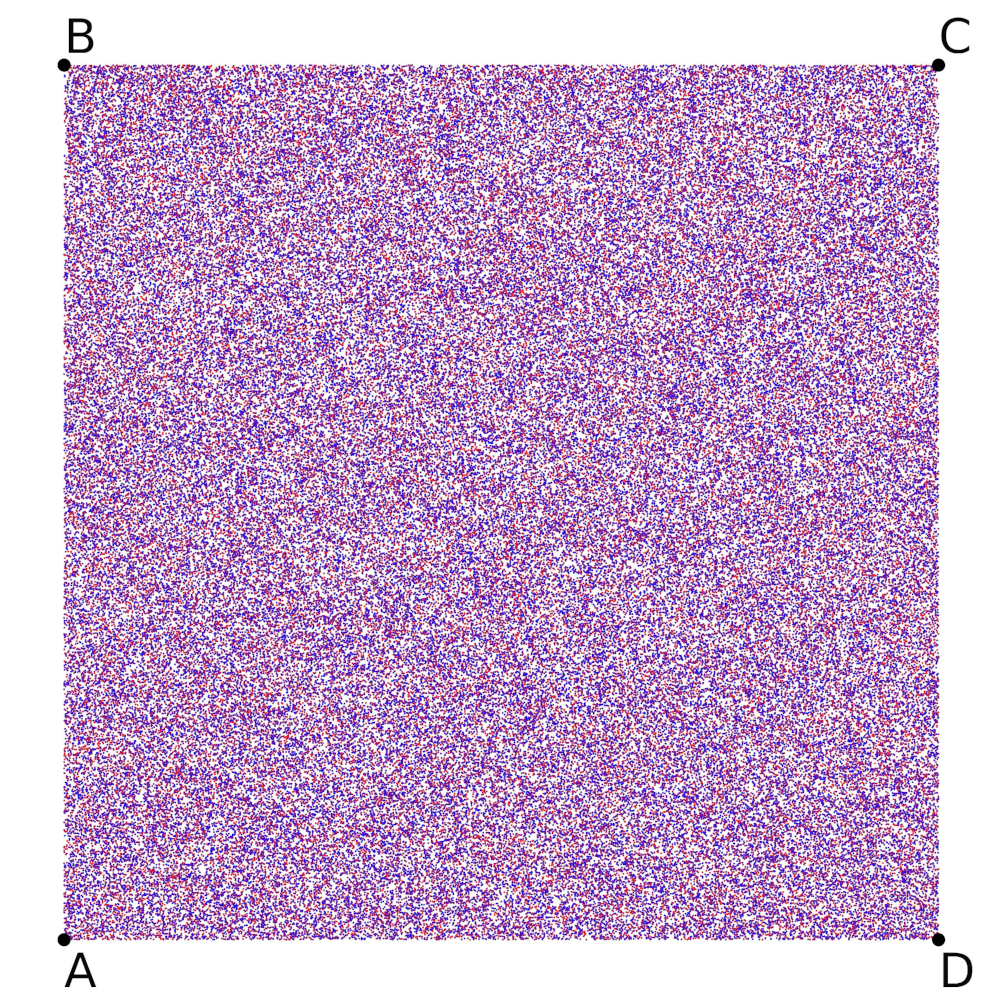Square Chaos Game

As a reminder, the Hutchinson operator is a set of functions that act on a point in space, , and return another another point at a new location. These functions are meant to be used over and over again in some fashion, and as you continually iterate through them, some shape will eventually be drawn. This shape is known as an attractor, and the entire system is called an iterated function system due to the iterative nature of drawing the attractor.

In these cases, each function will move the point to be halfway between its original position and the position of , , , and for , , , and , respectively. Even though , , and are the same for both attractors, the addition of drastically changes the final result! It is surprising that two seemingly identical sets of functions can look so different in the end, and this leads us to a somewhat challenging question: given a set of functions, is there any way to predict what the attractor will be without iterating through the functions?

In general, the answer is no. You must sample the function set in some fashion to get find the resulting attractor.

This feels somewhat unsettling to me. After all, each individual function is simple, so why is the result so difficult to predict? In this chapter, I hope to provide a slightly more satisfying answer by introducing another iterated function system with beautiful attractor, known as the Barnsley fern [1]:

Hutchinson Operator Attractor
Barnsley Chaos Game

At first glance, this set of functions looks like an incomprehensible mess of magic numbers to create a specific result, and in a sense, that is precisely correct. That said, we will go through each function and explain how it works, while also providing a simple chaos game implementation in code. By the end of this chapter, we do not hope to provide a general strategy for understanding all iterated function systems, but we hope to at least make this one set of functions a bit more understandable.

Individual affine transforms

The first thing to note about the Barnsley set of functions is that each one is an affine transformation. Though it is not a hard rule, most iterated function systems use affine transforms, so this notation is common. In fact, the Sierpinski operators can also be written in an affine form:

Non-affine Affine

The affine variant performs the same operation by scaling the and component of by and then adding half of either , , or for , , or , respectively. Each of these transforms involves some linear component (scaling or shearing) with an additional translation.

As an important side-note: in both the Barnsley and Sierpinski function systems, the coefficients of the transformation matrix are all less than 1. This property is known as contractivity, and an iterated function system can only have an attractor if the system is contractive. Upon reflection, this makes sense. If the matrix elements were greater than 1, the point could tend towards infinity after successive iterations of the function.

Now let's hop into disecting the Barnsley fern by seeing how each transform affects a random distribution of points:

Function Operation

This operation moves every point to a single line.

This operation moves every point up and to the right.

This operation rotates every point to the left.

This operation flips every point and rotates to the right.

At this stage, it might be clear what is going on, but it's not exactly obvious. Essentially, each operation corresponds to another part of the fern:

  • creates the stem.
  • creates successively smaller ferns moving up and to the right.
  • creates the leaves on the right.
  • creates the leaves on the left.

The easiest way to make sense of this is to show the operations on the Barnsley fern, itself, instead of a random distribution of points.

Function Operation

Here, the self-similar nature of the fern becomes apparent. Each operation is effectively moving a point on one part of the fern to a point on another part of the fern.

In the final construction, it is clear that fewer points are necessary on some parts than others. The stem, for example, does not need many points at all. Meanwhile, the bulk of the fern seems to be generated by , so we probably want the majority of the points to choose that function when iterating through he set. To account for this, each function is also given a probability of being chosen:

Function Probability
0.01
0.85
0.07
0.07

Playing around a bit...

One big advantage of using affine transformations to construct an attractor is that mathematicians and programmers can leverage their knowledge of how these transformations work to also modify the resulting image. Here are a few examples of ferns that can be generated by modifying constituent functions:

Function Operation

where

Turning stems to leaves

where

Changing fern tilt

where

Plucking left leaves

where

Plucking right leaves

As an important note: the idea of modifying a resulting image by twiddling the knobs of an affine transform is the heart of many interesting methods, including fractal image compression where a low resolution version of an image is stored along with a reconstructing function set to generate high-quality images on-the-fly [2][3]. If this seems mystifying, don't worry! We'll definitely come back to this soon, I just wanted to briefly mention it now so it's on everyone's mind as we move forward.

Video Explanation

Here is a video describing the Barnsley fern:

Example Code

Similar to the chapter on iterated function systems, the example code here will show a chaos game for the construction of an attractor; however, in this case the attractor will be the Barnsley fern instead of the Sierpinski triangle. The biggest differences between the two code implementations is that the Barnsley implementation must take into account the varying probabilities for choosing each function path and that we will be choosing an initial point that is on the attractor this time (namely ).

using DelimitedFiles

# This is a function that reads in the Hutchinson operator and corresponding
#     probabilities and outputs a randomly selected transform
# This works by choosing a random number and then iterating through all 
#     probabilities until it finds an appropriate bin
function select_array(hutchinson_op, probabilities)

    # random number to be binned
    rnd = rand()

    # This checks to see if a random number is in a bin, if not, that 
    #     probability is subtracted from the random number and we check the
    #     next bin in the list
    for i = 1:length(probabilities)
        if (rnd < probabilities[i])
            return hutchinson_op[i]
        end
        rnd -= probabilities[i]
    end
end

# This is a general function to simulate a chaos game
# n is the number of iterations
# initial_location is the starting point of the chaos game
# hutchinson_op is the set of functions to iterate through
# probabilities is the set of probabilities corresponding to the likelihood
#     of choosing their corresponding function in hutchinson_op
function chaos_game(n::Int, initial_location, hutchinson_op, probabilities)

    # Initializing the output array and the initial point
    output_points = zeros(n,2)

    # extending point to 3D for affine transform
    point = [initial_location[1], initial_location[2], 1]

    for i = 1:n
        output_points[i,:] .= point[1:2]
        point = select_array(hutchinson_op, probabilities)*point
    end

    return output_points

end

barnsley_hutchinson = [[0.0 0.0 0.0;
                        0.0 0.16 0.0;
                        0.0 0.0 1.0],
                       [0.85 0.04 0.0;
                        -0.04 0.85 1.60;
                        0.0 0.0 1.0],
                       [0.20 -0.26 0.0;
                        0.23 0.22 1.60;
                        0.0 0.0 1.0],
                       [-0.15 0.28 0.0;
                        0.26 0.24 0.44;
                        0.0 0.0 1.0]]

barnsley_probabilities = [0.01, 0.85, 0.07, 0.07]
output_points = chaos_game(10000, [0,0],
                           barnsley_hutchinson, barnsley_probabilities)
writedlm("out.dat", output_points)

use rand::prelude::*;
#[derive(Clone, Copy)]
struct Point2 {
    x: f64,
    y: f64,
}

#[derive(Clone, Copy)]
struct Point3 {
    x: f64,
    y: f64,
    z: f64,
}

impl Point3 {
    fn new(x: f64, y: f64, z: f64) -> Self {
        Self { x, y, z }
    }

    fn matrix_mul(self, rhs: Vec<Point3>) -> Self {
        let x = rhs[0].x * self.x + rhs[0].y * self.y + rhs[0].z * self.z;
        let y = rhs[1].x * self.x + rhs[1].y * self.y + rhs[1].z * self.z;
        let z = rhs[2].x * self.x + rhs[2].y * self.y + rhs[2].z * self.z;
        Self::new(x, y, z)
    }
}

fn select_array(hutchinson_op: &[Vec<Point3>], probabilities: &[f64]) -> Vec<Point3> {
    let mut rng = rand::thread_rng();
    let mut rnd = rng.gen::<f64>();

    for (i, probability) in probabilities.iter().enumerate() {
        if rnd < *probability {
            return hutchinson_op[i].clone();
        }
        rnd -= probability;
    }

    return vec![];
}

fn chaos_game(
    iters: usize,
    initial_location: Point2,
    hutchinson_op: &[Vec<Point3>],
    probabilities: &[f64],
) -> Vec<Point2> {
    let mut point = Point3 {
        x: initial_location.x,
        y: initial_location.y,
        z: 1.0,
    };
    (0..iters)
        .into_iter()
        .map(|_| {
            let old_point = point;
            let operation = select_array(hutchinson_op, probabilities);
            point = point.matrix_mul(operation);
            Point2 {
                x: old_point.x,
                y: old_point.y,
            }
        })
        .collect()
}

fn main() {
    let barnsley_hutchinson = vec![
        vec![
            Point3::new(0.0, 0.0, 0.0),
            Point3::new(0.0, 0.16, 0.0),
            Point3::new(0.0, 0.0, 1.0),
        ],
        vec![
            Point3::new(0.85, 0.04, 0.0),
            Point3::new(-0.04, 0.85, 1.60),
            Point3::new(0.0, 0.0, 1.0),
        ],
        vec![
            Point3::new(0.20, -0.26, 0.0),
            Point3::new(0.23, 0.22, 1.60),
            Point3::new(0.0, 0.0, 1.0),
        ],
        vec![
            Point3::new(-0.15, 0.28, 0.0),
            Point3::new(0.26, 0.24, 0.44),
            Point3::new(0.0, 0.0, 1.0),
        ],
    ];

    let barnsley_probabilities = vec![0.01, 0.85, 0.07, 0.07];

    let mut out = String::new();

    for point in chaos_game(
        10_000,
        Point2 { x: 0.0, y: 0.0 },
        &barnsley_hutchinson,
        &barnsley_probabilities,
    ) {
        out += format!("{}\t{}\n", point.x, point.y).as_str();
    }

    std::fs::write("./out.dat", out).unwrap();
}

// The code bellow uses C++-17 features, compile it with C++-17 flags, e.g.:
// clang++ -Wall -Wextra -Wshadow -Wnon-virtual-dtor -Wold-style-cast -Wcast-align -Wunused -Woverloaded-virtual -Wpedantic -Wconversion -Wsign-conversion -Wnull-dereference -Wdouble-promotion -Wformat=2 -gdwarf-3 -D_GLIBCXX_DEBUG -std=c++17 -O3 -c ./barnsley.cpp barnsley

#include <array>
#include <cassert>
#include <fstream>
#include <random>

using Vec2 = std::array<double, 2>;
using Vec3 = std::array<double, 3>;
using Row = std::array<double, 3>;
using Op = std::array<Row, 3>;

constexpr auto OpN = 4U;

template <size_t N>
auto operator+(std::array<double, N> x, std::array<double, N> y) {
  for (auto i = 0U; i < N; ++i)
    x[i] += y[i];
  return x;
}

template <size_t N>
auto operator*(double k, std::array<double, N> v) {
  for (auto i = 0U; i < N; ++i)
    v[i] *= k;
  return v;
}

template <size_t N>
auto operator*(std::array<double, N> v, double k) {
  return k * v;
}

auto operator*(const Op& x, const Vec3& y) {
  auto ret = Vec3{};
  for (auto i = 0U; i < 3U; ++i) {
    ret[i] = 0;
    for (auto j = 0U; j < 3U; ++j)
      ret[i] += y[j] * x[i][j];
  }
  return ret;
}

// Returns a pseudo-random number generator
std::default_random_engine& rng() {
  // Initialize static pseudo-random engine with non-deterministic random seed
  static std::default_random_engine randEngine(std::random_device{}());
  return randEngine;
}

// Returns a random double in [0, 1)
double drand() {
  return std::uniform_real_distribution<double>(0.0, 1.0)(rng());
}

// This is a function that reads in the Hutchinson operator and
// corresponding
//     probabilities and outputs a randomly selected transform
// This works by choosing a random number and then iterating through all
//     probabilities until it finds an appropriate bin
auto select_array(
    const std::array<Op, OpN>& hutchinson_op,
    const std::array<double, OpN>& probabilities) {

  // random number to be binned
  auto rnd = drand();

  // This checks to see if a random number is in a bin, if not, that
  //     probability is subtracted from the random number and we check the
  //     next bin in the list
  for (auto i = 0U; i < probabilities.size(); ++i) {
    if (rnd < probabilities[i])
      return hutchinson_op[i];
    rnd -= probabilities[i];
  }
  assert(!static_cast<bool>("check if probabilities adding up to 1"));
  return hutchinson_op[0];
}

// This is a general function to simulate a chaos game
// n is the number of iterations
// initial_location is the the starting point of the chaos game
// hutchinson_op is the set of functions to iterate through
// probabilities is the set of probabilities corresponding to the likelihood
//     of choosing their corresponding function in hutchinson_op
auto chaos_game(
    size_t n,
    Vec2 initial_location,
    const std::array<Op, OpN>& hutchinson_op,
    const std::array<double, OpN>& probabilities) {

  // Initializing the output array and the initial point
  auto output_points = std::vector<Vec2>{};

  // extending point to 3D for affine transform
  auto point = Vec3{initial_location[0], initial_location[1], 1};

  for (auto i = 0U; i < n; ++i) {
    output_points.push_back(Vec2{point[0], point[1]});
    point = select_array(hutchinson_op, probabilities) * point;
  }

  return output_points;
}

int main() {

  const std::array barnsley_hutchinson = {
      Op{Row{0.0, 0.0, 0.0}, Row{0.0, 0.16, 0.0}, Row{0.0, 0.0, 1.0}},
      Op{Row{0.85, 0.04, 0.0}, Row{-0.04, 0.85, 1.60}, Row{0.0, 0.0, 1.0}},
      Op{Row{0.20, -0.26, 0.0}, Row{0.23, 0.22, 1.60}, Row{0.0, 0.0, 1.0}},
      Op{Row{-0.15, 0.28, 0.0}, Row{0.26, 0.24, 0.44}, Row{0.0, 0.0, 1.0}}};

  const std::array barnsley_probabilities = {0.01, 0.85, 0.07, 0.07};
  auto output_points = chaos_game(
      10'000, Vec2{0, 0}, barnsley_hutchinson, barnsley_probabilities);

  std::ofstream ofs("out.dat");
  for (auto pt : output_points)
    ofs << pt[0] << '\t' << pt[1] << '\n';
}

#include <stdio.h>
#include <stdlib.h>

struct matrix {
    double xx, xy, xz,
           yx, yy, yz,
           zx, zy, zz;
};

struct point2d {
    double x, y;
};

struct point3d {
    double x, y, z;
};

struct point3d matmul(struct matrix mat, struct point3d point)
{
    struct point3d out = {
        mat.xx * point.x + mat.xy * point.y + mat.xz * point.z,
        mat.yx * point.x + mat.yy * point.y + mat.yz * point.z,
        mat.zx * point.x + mat.zy * point.y + mat.zz * point.z
    };
    return out;
}

// This function reads in the Hutchinson operator and corresponding
// probabilities and returns a randomly selected transform
// This works by choosing a random number and then iterating through all
// probabilities until it finds an appropriate bin
struct matrix select_array(struct matrix *hutchinson_op, double *probabilities,
                           size_t num_op)
{
    // random number to be binned
    double rnd = (double)rand() / RAND_MAX;

    // This checks to see if a random number is in a bin, if not, that
    // probability is subtracted from the random number and we check the next
    // bin in the list
    for (size_t i = 0; i < num_op; ++i) {
        if (rnd < probabilities[i]) {
            return hutchinson_op[i];
        }
        rnd -= probabilities[i];
    }
    return hutchinson_op[0];
}

// This is a general function to simulate a chaos game
//  - output_points: pointer to an initialized output array
//  - num: the number of iterations
//  - initial_point: the starting point of the chaos game
//  - hutchinson_op: the set of functions to iterate through
//  - probabilities: the set of probabilities corresponding to the likelihood
//      of choosing their corresponding function in hutchingson_op
//  - nop: the number of functions in hutchinson_op
void chaos_game(struct point2d *output_points, size_t num,
                struct point2d initial_point, struct matrix *hutchinson_op,
                double *probabilities, size_t nop)
{
    // extending point to 3D for affine transform
    struct point3d point = {initial_point.x, initial_point.y, 1.0};

    for (size_t i = 0; i < num; ++i) {
        point = matmul(select_array(hutchinson_op, probabilities, nop), point);
        output_points[i].x = point.x;
        output_points[i].y = point.y;
    }
}

int main()
{
    struct matrix barnsley_hutchinson[4] = {
        {
            0.0, 0.0, 0.0,
            0.0, 0.16, 0.0,
            0.0, 0.0, 1.0
        },
        {
            0.85, 0.04, 0.0,
            -0.04, 0.85, 1.60,
            0.0, 0.0, 1.0
        },
        {
            0.2, -0.26, 0.0,
            0.23, 0.22, 1.60,
            0.0, 0.0, 1.0
        },
        {
            -0.15, 0.28, 0.0,
            0.26, 0.24, 0.44,
            0.0, 0.0, 1.0
        }
    };

    double barnsley_probabilities[4] = {0.01, 0.85, 0.07, 0.07};
    struct point2d output_points[10000];
    struct point2d initial_point = {0.0, 0.0};
    chaos_game(output_points, 10000, initial_point, barnsley_hutchinson,
               barnsley_probabilities, 4);
    FILE *f = fopen("barnsley.dat", "w");
    for (size_t i = 0; i < 10000; ++i) {
        fprintf(f, "%f\t%f\n", output_points[i].x, output_points[i].y);
    }
    fclose(f);

    return 0;
}

import java.io.FileWriter;
import java.io.IOException;
import java.util.Random;

public class Barnsley {

    private static class Point {
        public double x, y, z;

        public Point(double x, double y, double z) {
            this.x = x;
            this.y = y;
            this.z = z;
        }

        public Point(double[] coordinates) {
            this.x = coordinates[0];
            this.y = coordinates[1];
            this.z = coordinates[2];
        }

        public Point matrixMultiplication(double[][] matrix) {
            double[] results = new double[3];
            for (int i = 0; i < 3; i++) {
                results[i] = matrix[i][0] * x + matrix[i][1] * y + matrix[i][2] * z;
            }
            return new Point(results);
        }
    }

    // This is a function that reads in the Hutchinson operator and corresponding
    //   probabilities and outputs a randomly selected transform
    // This works by choosing a random number and then iterating through all
    //   probabilities until it finds an appropriate bin
    public static double[][] selectArray(double[][][] hutchinsonOp, double[] probabilities) {
        Random rng = new Random();
        // Random number to be binned
        double rand = rng.nextDouble();

        // This checks to see if a random number is in a bin, if not, that
        // probability is subtracted from the random number and we check the
        // next bin in the list
        for (int i = 0; i < probabilities.length; i++) {
            if (rand < probabilities[i])
                return hutchinsonOp[i];
            rand -= probabilities[i];
        }
        // This return will never be reached, as the loop above ensures that at some point rand will be smaller
        // than a probability. However, Java does not know this and thus this return is needed for compilation.
        return null;
    }

    // This is a general function to simulate a chaos game
    // n is the number of iterations
    // initialLocation is the starting point of the chaos game
    // hutchinsonOp is the set of functions to iterate through
    // probabilities is the set of probabilities corresponding to the likelihood
    //   of choosing their corresponding function in hutchinsonOp
    public static Point[] chaosGame(int n, Point initialLocation, double[][][] hutchinsonOp, double[] probabilities) {
        // Initializing output points
        Point[] outputPoints = new Point[n];
        Point point = initialLocation;

        for (int i = 0; i < n; i++) {
            outputPoints[i] = point;
            point = point.matrixMultiplication(selectArray(hutchinsonOp, probabilities));
        }

        return outputPoints;
    }

    public static void main(String[] args) {
        double[][][] barnsleyHutchinson = {
                {{0.0, 0.0, 0.0},
                 {0.0, 0.16, 0.0},
                 {0.0, 0.0, 1.0}},
                {{0.85, 0.04, 0.0},
                 {-0.04, 0.85, 1.60},
                 {0.0, 0.0, 1.0}},
                {{0.20, -0.26, 0.0},
                 {0.23, 0.22, 1.60},
                 {0.0, 0.0, 1.0}},
                {{-0.15, 0.28, 0.0},
                 {0.26, 0.24, 0.44},
                 {0.0, 0.0, 1.0}}
        };
        double[] barnsleyProbabilities = new double[]{0.01, 0.85, 0.07, 0.07};
        Point[] outputPoints = chaosGame(10000, new Point(0.0, 0.0, 1.0), barnsleyHutchinson, barnsleyProbabilities);
        try (FileWriter fw = new FileWriter("barnsley.dat")) {
            for (Point p : outputPoints) {
                fw.write(p.x + "\t" + p.y + "\n");
            }
        } catch (IOException e) {
            e.printStackTrace();
        }
    }

}

from random import choices
import numpy as np

data Point(x=0, y=0):
    def __rmatmul__(self, mat: np.array):
        point_array = np.array([self.x, self.y, 1])
        x, y, *_ = tuple(*(mat @ point_array))
        return Point(x, y)


def chaos_game(Point(initial_location), hutchinson_op, probabilities):
    point = initial_location
    while True:
        yield (point := choices(hutchinson_op, probabilities) @ point)

barnsley_hutchinson = [
    np.array([
        [0., 0., 0.],
        [0., 0.16, 0.],
        [0., 0., 1.],
    ]),
    np.array([
        [0.85, 0.04, 0.],
        [-0.04, 0.85, 1.6],
        [0., 0., 1.],
    ]),
    np.array([
        [0.2, -0.26, 0.],
        [0.23, 0.22, 1.6],
        [0., 0., 1.],
    ]),
    np.array([
        [-0.15, 0.28, 0.],
        [0.26, 0.24, 0.44],
        [0., 0., 1.],
    ]),
]

barnsley_probabilities = [0.01, 0.85, 0.07, 0.07]

if __name__ == '__main__':
    output_gen = chaos_game(Point(0, 0), barnsley_hutchinson, barnsley_probabilities)
    output_points = np.array([*output_gen$[:10000]])
    np.savetxt("out.dat", output_points)

import Data.Array (Array, bounds, elems, listArray, (!))
import Data.List (intercalate)
import System.Random

data Point = Point Double Double

chaosGame :: RandomGen g => g -> Int -> Array Int (Double, (Point -> Point)) -> [Point]
chaosGame g n hutchinson = take n points
  where
    (x, g') = random g
    (y, g'') = random g'

    cumulProbabilities = scanl1 (+) $ map fst $ elems hutchinson
    to_choice x = length $ takeWhile (x >) cumulProbabilities

    picks = map to_choice $ randomRs (0, 1) g''
    step = fmap snd hutchinson

    points = Point x y : zipWith (step !) picks points

affine :: (Double, Double, Double, Double) -> (Double, Double) -> Point -> Point
affine (xx, xy, yx, yy) (a, b) (Point x y) = Point (a + xx * x + xy * y) (b + yx * x + yy * y)

showPoint :: Point -> String
showPoint (Point x y) = show x ++ "\t" ++ show y

main :: IO ()
main = do
  g <- newStdGen
  let barnsley =
        listArray
          (0, 3)
          [ (0.01, affine (0, 0, 0, 0.16) (0, 0)),
            (0.85, affine (0.85, 0.04, -0.04, 0.85) (0, 1.6)),
            (0.07, affine (0.2, -0.26, 0.23, 0.22) (0, 1.6)),
            (0.07, affine (-0.15, 0.28, 0.26, 0.24) (0, 0.44))
          ]
      points = chaosGame g 100000 barnsley

  writeFile "out.dat" $ intercalate "\n" $ map showPoint points

Bibliography

1.
Barnsley, Michael F, Fractals everywhere, Academic press, 2014.
2.
Wikipedia: Fractal Compression, 2019.
3.
Saupe, Dietmar and Hamzaoui, Raouf, A review of the fractal image compression literature, ACM, 1994.

License

Code Examples

The code examples are licensed under the MIT license (found in LICENSE.md).

Text

The text of this chapter was written by James Schloss and is licensed under the Creative Commons Attribution-ShareAlike 4.0 International License.

Images/Graphics

results matching ""

    No results matching ""